對數的真數只能是正數?

    一般的高中課本說對數的真數僅局限於正數的範圍，那麼，難道真數不是正數，就無法取對數了嗎？其實不然，不管真數是正數、負數、甚至拓展到複數，都是可以取對數的。

對數定義：

x^a=b，則定義log_xb=a

有就是「b是x的a次方」

b稱為「真數」，x稱為「底數」

一般來說，真數要大於是有原因的

考慮函數y=log x (一般不寫底數代表底數為10)

函數圖形如圖所示

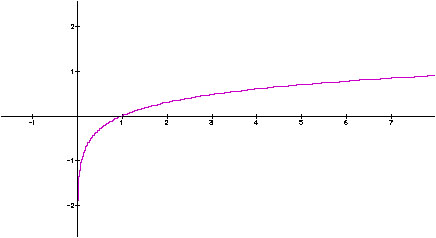
若x＜0，y就沒有值可以對應

所以才說x一定要大於0

但是，若是擴展到複數，就可以定義出真數為任何實數、複數的對數了

如何測量地球質量

地球質量大約5.97*10^24kg，那麼要如何測量出來呢？總不可能拿秤來量吧！將在此介紹三種測量地球質量的方法：

(1).卡文迪西(Herny Cavendish)在18世紀做了個有名的實驗，用精密的儀器，測出了萬有引力常數的值(6.67×10^-11×m³×kg×^-2×s^-1)，由此就能由牛頓的萬有引力定律推出地球的質量了。

簡諧運動 part3

    再來就是簡諧運動的實例了。其實簡諧運動的實例太多了──圓周運動的投影、小擺角的單擺、U型管的液體震盪、水面浮體的上下移動、彈簧的振動……不勝枚舉，但是，我要在這裡介紹另一個比較特別的例子。

簡諧運動 part2

其實，簡諧運動的函數最基礎並不是圓周運動投影，那只算是應用罷了。簡諧運動，可以描寫成下面的這個二階微分方程：

簡諧運動 part1

 簡諧運動（Simple Harmonic Motion , SHM），是自然界最簡單，最諧調的振動，所以稱之為「簡諧運動」。簡諧運動可以是為一個圓周運動對x（或是y）軸上的投影。簡諧運動有些比較常見的：彈簧的振動、水的上下震動、U形管的振盪、圓周運動投影、單擺小角度擺動等，都是常見的簡諧運動。

    簡諧運動若以圓周運動投影到x軸來看，可以寫出三條方程式

x(t)=Rcos(ωt+ψ)

v(t)=-Rωsin(ωt+ψ)

a(t)=-Rω²cos(ωt+ψ)

（R為振幅、ω為圓周運動的角速度、t為經過的時間、ψ為初始角度）

功能原理

理化組─電磁學實驗

理化組最近做了個有趣的電磁學實驗，在電池下方貼兩個強力磁鐵（我們是用NdFeB，釹鐵硼磁鐵，就是一般銀色小粒的強力磁鐵），再把漆包線摺成類似心型的形狀，把心型的凹下處和兩端的漆磨掉，小心的把心型的凹處放在電池正極上，下面兩條端點要輕觸磁鐵。結果漆包線就會在電池上自轉！

實驗示意圖

為什麼重力是平方反比而不是立方反比?

若在座標原點上，有一個質點，則此質點會在這個空間中產生一個重力場，以輻射狀向外發散，因為重力場是由此質點所產生，所以可以說此質點為本重力場的「起點」。

    在充斥著力場的空間中，做一個小球，則在這個封閉球面上，會有場經過。若是向內進去的量等於向外出去的量，則稱此處的「散度」為零；若是向內進去的量大於向外出去的量，則此處的「散度」小於零；若是向內進去的量小於向外出去的量，則此處的「散度」大於零。通常，我們是求某一點的散度，只要想像一球包住此點，並讓這顆球的半徑趨近於零，就可以算出此點的散度了。

自由落體秒數與下降距離曲線圖

自由落體秒數與下降距離曲線圖